最近，打算将算法作为自己以后的方向，故读了一些算法方面的文献，弄清楚了KNN与K-MEANS的不同，写一篇博文以备待查。
KNN
KNN是k-nearest neighbors algorithm的简称，又称为K近邻算法。
算法思路：如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。
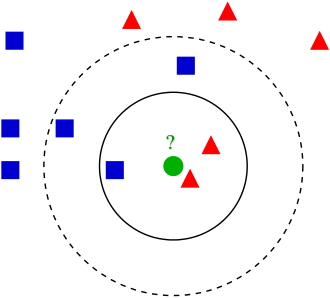上图中的蓝色的正方形和红色的三角形是已经分好类的两类数据，即带标签的数据，绿色的圆形是待确定类别的数据。
使用KNN算法确定该圆形的类别，如果K值为3，距离该圆形图标最近的3个点中，2个是三角形，1个是正方形，因此圆形属于三角形类别；但如果K值取5，情况发生了变化，离圆形最近的5个点中有2个三角形，3个正方形，所以圆形属于正方形类别。
K-MEANS
K-MEANS算法是聚类分析中使用最广泛的算法之一。它把n个对象根据他们的属性分为k个聚类以便使得所获得的聚类满足：同一聚类中的对象相似度较高；而不同聚类中的对象相似度较小。 算法思想：以空间中k个点为中心进行聚类，对最靠近他们的对象归类，通过迭代的方法，逐次更新各聚类中心的值，直到得到最好的聚类结果。 算法描述： （1）适当选择c个类的初始中心； （2）在第k次迭代中，对任意一个样本，求其到c各中心的距离，将该样本归到距离最短的那个中心所在的类； （3）利用均值等方法更新该类的中心值； （4）对于所有的C个聚类中心，如果利用（2）（3）的迭代法更新后，值保持不变，则迭代结束；否则继续迭代。
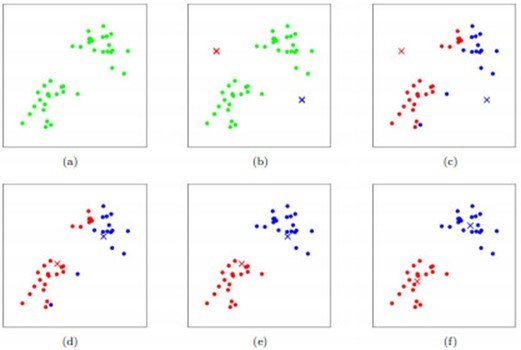如图所示，数据样本用圆点表示，每个簇的中心点用叉叉表示。(a)刚开始时是原始数据，杂乱无章，没有label，看起来都一样，都是绿色的。(b)假设数据集可以分为两类，令K=2，随机在坐标上选两个点，作为两个类的中心点。(c-f)演示了聚类的两种迭代。先划分，把每个数据样本划分到最近的中心点那一簇；划分完后，更新每个簇的中心，即把该簇的所有数据点的坐标加起来去平均值。这样不断进行”划分—更新—划分—更新”，直到每个簇的中心不在移动为止。
算法比较
| 名称 | KNN | K-Means |
|---|---|---|
| 目的 | 为了确定一个点的分类 | 为了将一系列点集分成k类 |
| 算法类别 | 分类算法 | 聚类算法 |
| 分类方法 | 监督学习，分类目标事先已知 | 非监督学习，将相似数据归到一起从而得到分类，没有外部分类 |
| 数据集特点 | 训练数据集有label，已经是完全正确的数据 | 训练数据集无label，是杂乱无章的，经过聚类后才变得有点顺序，先无序，后有序 |
| 是否需要训练 | 没有明显的前期训练过程，属于memory-based learning | 有明显的前期训练过程 |
| K值的意义 | “k”是用来计算的相邻数据数。来了一个样本x，要给它分类，即求出它的y，就从数据集中，在x附近找离它最近的K个数据点，这K个数据点，类别c占的个数最多，就把x的label设为c | K的含义：“k”是类的数目。K是人工固定好的数字，假设数据集合可以分为K个簇，由于是依靠人工定好，需要一点先验知识 |
| K对结果的影响 | K值确定后每次结果固定 | K值确定后每次结果可能不同，从 n个数据对象任意选择 k 个对象作为初始聚类中心，随机性对结果影响较大 |
| 时间复杂度 | O（n） | O(n*k*t)，t为迭代次数 |
代码
KNN
from numpy import *
import operator
#定义KNN算法分类器函数
#函数参数包括：(测试数据，训练数据，分类,k值)
def classify(inX,dataSet, labels, k):
dataSetSize = dataSet.shape[0]
diffMat = tile(inX,(dataSetSize,1))-dataSet
sqDiffMat=diffMat**2
sqDistances=sqDiffMat.sum(axis=1)
distances=sqDistances**0.5 #计算欧式距离
sortedDistIndicies=distances.argsort() #排序并返回index
#选择距离最近的k个值
classCount={}
for i in range(k):
voteIlabel=labels[sortedDistIndicies[i]]
#D.get(k[,d]) -> D[k] if k in D, else d. d defaults to None.
classCount[voteIlabel]=classCount.get(voteIlabel,0)+1
#排序
sortedClassCount=sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
return sortedClassCount[0][0]
#定义一个生成“训练样本集”的函数，包含特征和分类信息
def createDataSet():
group=array([[1,1.1],[1,1],[0,0],[0,0.1]])
labels=['A','A','B','B']
return group,labels
#生成训练样本
group,labels=KNN.createDataSet()
#对测试数据[0,0]进行KNN算法分类测试
KNN.classify([0,0],group,labels,3)
Out[3]: 'B'
K-MEANS
from numpy import *
import time
import matplotlib.pyplot as plt
# calculate Euclidean distance
def euclDistance(vector1, vector2):
return sqrt(sum(power(vector2 - vector1, 2)))
# init centroids with random samples
def initCentroids(dataSet, k):
numSamples, dim = dataSet.shape
centroids = zeros((k, dim))
for i in range(k):
index = int(random.uniform(0, numSamples))
centroids[i, :] = dataSet[index, :]
return centroids
# k-means cluster
def kmeans(dataSet, k):
numSamples = dataSet.shape[0]
# first column stores which cluster this sample belongs to,
# second column stores the error between this sample and its centroid
clusterAssment = mat(zeros((numSamples, 2)))
clusterChanged = True
## step 1: init centroids
centroids = initCentroids(dataSet, k)
while clusterChanged:
clusterChanged = False
## for each sample
for i in xrange(numSamples):
minDist = 100000.0
minIndex = 0
## for each centroid
## step 2: find the centroid who is closest
for j in range(k):
distance = euclDistance(centroids[j, :], dataSet[i, :])
if distance < minDist:
minDist = distance
minIndex = j
## step 3: update its cluster
if clusterAssment[i, 0] != minIndex:
clusterChanged = True
clusterAssment[i, :] = minIndex, minDist**2
## step 4: update centroids
for j in range(k):
pointsInCluster = dataSet[nonzero(clusterAssment[:, 0].A == j)[0]]
centroids[j, :] = mean(pointsInCluster, axis = 0)
print 'Congratulations, cluster complete!'
return centroids, clusterAssment
# show your cluster only available with 2-D data
def showCluster(dataSet, k, centroids, clusterAssment):
numSamples, dim = dataSet.shape
if dim != 2:
print "Sorry! I can not draw because the dimension of your data is not 2!"
return 1
mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', '<r', 'pr']
if k > len(mark):
print "Sorry! Your k is too large! please contact Zouxy"
return 1
# draw all samples
for i in xrange(numSamples):
markIndex = int(clusterAssment[i, 0])
plt.plot(dataSet[i, 0], dataSet[i, 1], mark[markIndex])
mark = ['Dr', 'Db', 'Dg', 'Dk', '^b', '+b', 'sb', 'db', '<b', 'pb']
# draw the centroids
for i in range(k):
plt.plot(centroids[i, 0], centroids[i, 1], mark[i], markersize = 12)
plt.show()
#调用函数
from numpy import *
import time
import matplotlib.pyplot as plt
## step 1: load data
print "step 1: load data..."
dataSet = []
fileIn = open('E:/Python/Machine Learning in Action/testSet.txt')
for line in fileIn.readlines():
lineArr = line.strip().split('\t')
dataSet.append([float(lineArr[0]), float(lineArr[1])])
## step 2: clustering...
print "step 2: clustering..."
dataSet = mat(dataSet)
k = 4
centroids, clusterAssment = kmeans(dataSet, k)
## step 3: show the result
print "step 3: show the result..."
showCluster(dataSet, k, centroids, clusterAssment)
#调用数据的格式
1.658985 4.285136
-3.453687 3.424321
4.838138 -1.151539
-5.379713 -3.362104
0.972564 2.924086
-3.567919 1.531611
0.450614 -3.302219
-3.487105 -1.724432
引用文献：chlele0105的专栏
HuangQinJian
孤独de雨
Wikipedia
芝士就是力量
moxigandashu的博客
chlele0105的专栏
zouxy09的专栏
